No Generalization without Understanding and Explanation – Communications of the ACM

McCarthy and his Prediction Regarding ‘Scruffy’ AI

John McCarthy, one of the founders of (and the one who supposedly coined the term) artificial intelligence (AI), stated on several occasions that if we insist on building AI systems based on empirical methods (e.g., neural networks or evolutionary models), we might be successful in building “some kind of an AI,” but even the designers of such systems will not understand how such systems work (see, for an example, [1]). In hindsight, this was an amazing prediction, since the deep neural networks (DNNs) that currently dominate AI are utterly unexplainable, and their unexplainability is paradigmatic: there are no concepts and human-understandable features in distributed connectionist architectures but microfeatures that are conceptually and cognitively hollow, not to mention that these microfeatures are semantically meaningless. In contrast with the bottom-up data-driven approach, McCarthy spent his career advocating logical approaches that are essentially top-down model driven (or theory-driven) approaches. McCarthy’s observation about the unexplainability of empirical data-driven approaches is rooted in the long philosophical tradition of linking explainability, understanding, and generalization (see [4], [5], and [6] for discussions on the relationship between understanding and explanation in science). I will briefly discuss these concepts below, before I come back and suggest what, in our opinion, is wrong with insisting on reducing AI to a data-driven machine learning paradigm.

Generalization, Explanation, and Understanding

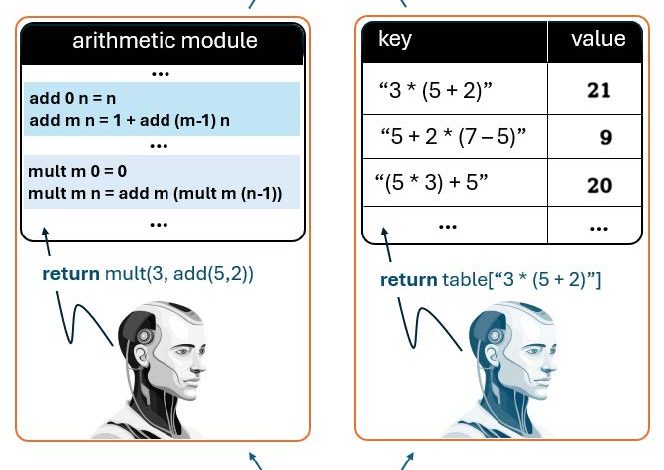
To consider the relationship between generalization, explanation, and understanding, let us consider an example. Suppose we have two intelligent agents, AG1 and AG2, and suppose we ask both to evaluate the expression “3 * (5 + 2).” Let us also suppose that AG1 and AG2 are two different “kinds” of robots. AG1 was designed by McCarthy and his colleagues, and thus it follows the rationalist approach in that its intelligence was built in a top-down, model- (or theory-) driven manner, while AG2’s intelligence was arrived at in a bottom-up data-driven (i.e., machine learning) approach (see Figure 1). Presumably, then, AG2 “learned” how to compute the value of arithmetic expressions by processing many training examples. As such, one can assume that AG2 has “encoded” these patterns in the weights of some neural network. To answer the query, all AG2 has to do is find something “similar” to 3 * (5 + 2) that it has encountered in the massive amount of data it was trained on. For simplicity, you can think of the memory of AG2 (with supposedly billions of parameters/weights) as a “fuzzy” hashtable. Once something ‘similar’ is detected, AG2 is ready to reply with an answer (essentially, it will do a look-up and find the most “similar” training example). AG1, on the other hand, has no such history, but has a model of how addition and multiplication work (perhaps as some symbolic function) and it can thus call the relevant modules to “compute” the expression according to the formal specification of the addition and multiplication functions.

In particular, AG1 knows that the result of (add m n) is adding m 1’s to n (or adding n 1’s to m – that is, it knows that addition is commutative). It also knows that multiplying m by n is essentially the result of adding m n times (or adding n m times, since multiplication is also commutative), while AG2 has no such knowledge. The advantage of AG2, as the (empirical/machine learning) argument goes, is that no one had to hand code the logic of addition and multiplication (as well as others) but it simply “learned” how to approximate these functions by “seeing” many examples during “training.” But AG2 has several problems.

Here is a summary of the main limitations of the empirical AG2:

1. AG2 does not “understand” how addition and multiplication work
2. Because of (1) AG2 cannot explain how or why 3 * (5 + 2) evaluates to 21
3. Because of (1) and (2), and while AG1 can, AG2 cannot (correctly and reliably) evaluate any expression that is out of distribution (OOD) of the data it has seen during “training”

Essentially, because the theory/model-driven AG1 “understands” the processes (i.e., because it “knows” how addition and multiplication work), it can explain its computation, while AG2 cannot and will always fail when asked to handle data that is out of distribution (OOD) of the examples it was trained on. Moreover, because AG1 “understands” how addition and multiplication work, it can generalize and compute the value of any arithmetic expression, because the logic of (add m n) and (mult m n) works for all m and for all n. Note, therefore, that to achieve understanding (and thus explanation and generalization) AG1 had to be a robot that can represent, manipulate, and reason with quantified symbolic variables. Such systems are not based on the “similarity” paradigm, but on object identity, while all AG2 can perform is object similarity (see [2] for a discussion on why DNNs cannot reason with object “identity” but only with the potentially circular “similarity”).

The moral of this introduction is this: an agent can “explain” a phenomenon or a process if it “understands” how it works, and vice versa (if I understand something, I can explain it — and if I can explain it, it means I understand it). Moreover, if I understand it and I can explain it, then I can generalize and handle similar situations, ad infinitum (again, see [4], [5], and [6]). Currently, and unfortunately, however, AI is dominated by what McCarthy feared, namely unexplainable systems that do not have sound logical foundations. But the issue here is not simply one of “elegance,” but is much deeper. The issue is that systems that are not based on “understanding” the phenomenon (the theory, or the underlying model) are not only unexplainable but, and more seriously, are systems that cannot ever get to true generalization because true generalization requires fully understanding the model/the theory and that, in turn, requires the representation and manipulation of symbolic and quantified variables that DNNs lack. This limitation might not show in the generative side of the equation, but it will show in problems that require reasoning such as genuine natural language understanding and planning, two tasks that even children master at a very young age. We discuss this below.

No Reasoning if there is no Understanding

The intricate relationship between generalization, explanation, and understanding, all of which are beyond the subsymbolic architecture of DNNs, show up in problems that require reasoning with quantified symbolic variables such as deep understanding of natural language, as well as simple problem solving such as that involved in planning. As an example, consider posing this simple planning problem to GPT 1o (the latest release that supposedly does advanced reasoning by implementing an internal chain of thought (CoT) loop):

If you try this (or any other configuration of the initial and final states), you will notice that what would take a young girl a few minutes to solve is beyond the reach of the multi-billion-dollar matrix multipliers (GPT-4o and GPT-1o). Not only is the final state never reached, but even the intermediate steps are nonsensical to the point where, given enough time, a monkey making random moves on the 8-tile square would probably do better (see this description of the “infinite monkey theorem”).

On the language side, these stochastic machines did not fare better. Figure 2 is an example where these systems will always fail. The underlying architecture of DNNs is purely extensional (roughly, operates by value only, and not by reference to symbols and concepts). Thus, for DNNs, two values that refer to the same object are always interchangeable. However, and although Guimarães is the ancient capital of Portugal, if “John wanted to know where the ancient capital of Portugal is located,” that does not mean (or it does not entail) that “John wanted to know where Guimarães is located.” (After all, like my uncle Constantine, John might not have a clue which city was the ancient capital of Portugal!)

Another problem, directly related to the above discussion on generalization, explanation, and understanding, is the out of distribution (OOD) problem and this also shows in problems related to true language understanding. One typical example is related to the linguistic phenomenon known by copredication which occurs when an entity (or a concept) is used in the same context to refer, at once, to several types of objects. As an example, consider the example below where the term “Barcelona” is used once to refer, simultaneously, to three different types of objects:

• I was visiting Barcelona when it won over Real Madrid and when it was getting ready to vote for independence.

In the sentence above ‘Barcelona’ is used to refer, at once, to: (i) the city (geographic location) I was visiting; (ii) to the Barcelona football team (that won over Real Madrid); and (iii) to the voting population of the city. All tested LLMs wrongly inferred that the geographic location is what won over Real Madrid and that the geographic location was voting for independence. The point is that these LLMs will always fail in inferring the implicit reference to additional entities that are not explicitly stated. The reason these systems fail in such examples is that the possible copredications that one can make are in theory infinite (and you cannot chase Chomsky’s infinity!) and thus such information will always be out of distribution (OOD) (see [3] for more examples on why stochastic text generators like GPT will always fail “true” language understanding in copredication and other linguistic phenomena, regardless of their impressive generative capabilities).

A Brief Summary

As impressive as LLMs are, at least in their generative capabilities, these systems will never be able to perform high-level reasoning, the kind that is needed in deep language understanding, problem solving, and planning. The reason for the qualitative “never” in the preceding sentence is that the (theoretical and technical) limitations we alluded to are not a function of scale or the specifics of the model or the training corpus. The problems we outlined above that preclude explanation, understanding, and generalization are a function of the underlying architecture of DNNs that can be summarized as follows:

1. DNNs are purely extensional models (and thus, they cannot cope with intensionality)
2. DNNs cannot make any (meaningful) predictions involving out of distribution data (OOD)
3. DNNs cannot decide on object identity — only object similarity (see [2])
4. DNNs cannot cope with problems that require reasoning with quantified symbolic variables
5. DNNs disperse computation into low-level microfeatures making them unexplainable

What (1) is saying is that DNNs are “by value” only architectures and thus they do not (and they cannot) cope with intensionality (with an “s”) which is rampant in language understanding (e.g., even though “Paris” = “the most populous city in France,” that equality might change at some point!). What (2) is saying is that we make many implicit relations in language that are never in any training set (language is infinite) and thus contexts that involve phenomena like copredication will never be properly understood. The problems in (3) and (4) are behind the reasons why DNNs cannot do planning — even simple cases like the toy example discussed above, because planning requires object identity and not just object similarity, and it also requires scope and quantification over symbolic variables. Finally, (5) is the reason why DNNs are hopelessly unexplainable — once the input components are distributed (crushed) into subcomponents the original components are lost and thus the output can never be explained in terms of the original components (or, technically speaking, DNNs lack structured semantics!).

Concluding remark

The above criticism of DNNs and LLMs is not intended to imply that empirical methods that perform data-driven learning do not have their place, because they do. There are plenty of applications where a bottom-up data-driven learning “module” is not only suitable, but might be the only appropriate method (e.g., image recognition). But this will be just one statistical pattern recognition module in a massive Minsky-style Society of Mind (or just one module in Fodor’s massive Modular Mind), where there are many other modules that do deductive and abductive inference, disambiguation, concept subsumption, planning, scene understanding, etc.

To insist on reducing the mind and human cognition to stochastic gradient descent and backpropagation is not only unscientific, but is also folly and potentially harmless.

References

1. John McCarthy, (2007), From here to human-level AI, Artificial Intelligence, 171, pp. 1174–1182
2. Jesse Lopes, (2023), Can Deep CNNs Avoid Infinite Regress/Circularity in Content Constitution? Minds and Machines 33, pp. 507–524
3. Walid Saba, (2024), Stochastic Text Generators do not Understand Language, but they can Help us Get There (in preparation, available here)
4. Michael Strevens, (2013), No Understanding without Explanation, Studies in History and Philosophy of Science, pp. 510-515.
5. Joseph J. Williams and Tania Lombrozo, (2009), The Role of Explanation in Discovery and Generalization: Evidence from Category Learning, Cognitive Science 34, pp. 776–806
6. Frank C. Keil, (2006), Explanation and Understanding, Annual Review of Psychology, Vol. 57:227-254.

Walid Saba is Senior Research Scientist at the Institute for Experiential AI at Northeastern University. He has published over 45 articles on AI and NLP, including an award-winning paper at KI-2008.